Глава 3. Обработка результатов эксперимента
Разбиение спектральных кривых на гауссианы
Нередко при обработке экспериментальных данных ставится задача аппроксимации исходного набора значений некой ожидаемой функциональной зависимостью (чаще всего прямой, экспонентой или логарифмом). При анализе спектров излучения или поглощения света для аппроксимации отдельного пика на спектре можно выбрать функцию Гаусса (статистическую функцию плотности нормального распределения) вида \( Y=\frac1{\sigma\sqrt {2\pi𝑒}} 𝑒^{-\frac{(х-\barх)^2}{2\sigma}} \), где \( \barх \) – математическое ожидание, σ – дисперсия. Покажем на примере этой функции, как можно с помощью Python решить задачу аппроксимации.
Для начала разнообразим ситуацию первичными данными: предположим, что результаты спектральных измерений записаны в электронную таблицу Microsoft Excel. В таком случае нам нужно найти метод для загрузки данных из xls-файла.
Для этого воспользуемся возможностями библиотеки openpyxl:
pip install openpyxl
В представленном на скриншоте файле spectra.xlsx, открытом в Мicrosoft Excel, видны две вкладки.
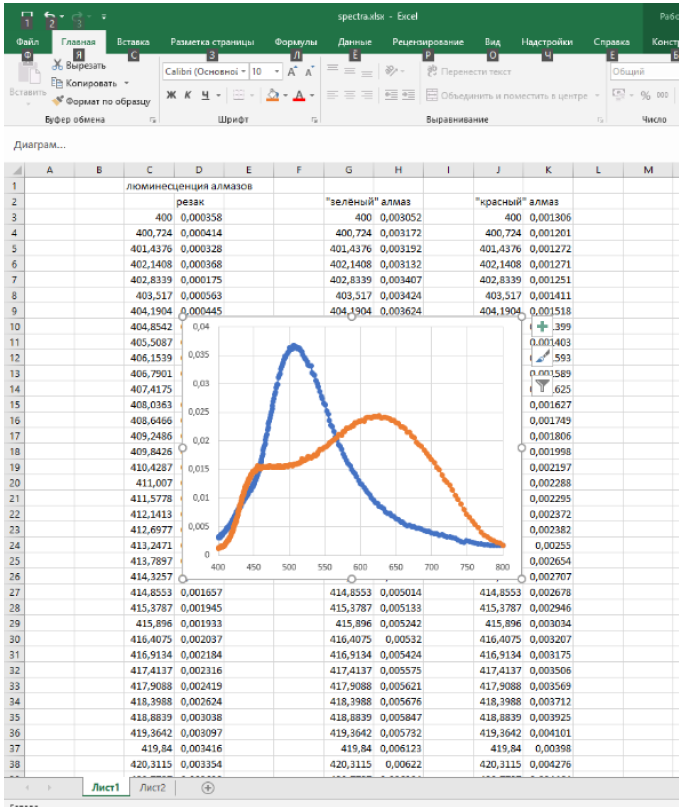
На вкладке Лист1 имеется несколько экспериментальных наборов данных для разных материалов. Нам потребуются данные из столбцов J (10) и K (11).
Ниже представлена программа на Python, загружающая данные из Excel-файла.
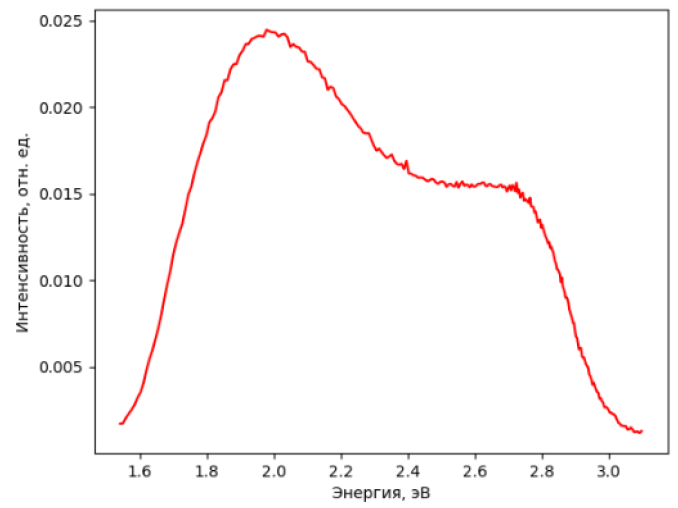
В строке 5 выводится на экран список всех листов книги Excel. Нужный лист выбираем по его имени в строке 6. Из десятого столбца таблицы считываем значения длин волн в нанометрах (строки таблицы с 3 по 270) и записываем в список X, предварительно переведя их в электронвольты (строка 10). Значения интенсивности считываем из столбца 11 и записываем в список Y (строка 11). Даже если в ячейках таблицы Excel будут не значения, а результаты вычислений по формулам, это не будет проблемой, поскольку используется опция value.
Рассмотрим теперь способ аппроксимации полученных данных суммой функций Гаусса. В случае с представленным выше спектром люминесценции достаточно сложной формы можно предположить, что свечение обусловлено дефектами разной природы, каждый из которых даёт пик, близкий по форме к статистическому распределению Гаусса. В данном случае как минимум два гауссиана составляют в сумме этот спектр. Напишем программу, которая решит поставленную задачу:
В стоках 7-8 определим функцию, описывающую статистическое распределение Гаусса. Параметр x – значение по абсциссе, а – нормировка по высоте, x0 – положение максимума,s – величина, пропорциональная полуширине.
Форма записи выражения в данном случае полностью совпадает с описанием функции Гаусса в приложении Curve Fitting Toolbox
Поскольку предполагается, что будут применяться групповые операции при работе с векторами (в стиле MATLAB), будем вычислять экспоненту в виде np.exp, и далее везде при работе с векторами будем также использовать библиотеку numpy. Функция DoubleGauss является суммой двух гауссианов и, соответственно, имеет шесть параметров, которые могут варьироваться для достижения наилучшей корреляции с экспериментальными данными.
Строки 16-21 полностью аналогичны предыдущему листингу и реализуют загрузку исходного набора данных. Собственно аппроксимация осуществляется в строке 24 с помощью метода curve_fit из библиотеки scipy. Эта библиотека в представленных примерах встретилась в первый раз, но на самом деле она содержит весьма обширный набор методов анализа данных и носит название Scientific Computing Tools for Python . Библиотека устанавливается в обычном порядке. Параметрами curve_fit являются аппроксимирующая функция, набор аппроксимируемых точек (списки X и Y), вектор начальных приближений p0, значение которого задано в строке 14, и кортеж ограничений по минимальным и максимальным значениям для всех варьируемых параметров. Следует заметить, что оба последних параметра очень важны и требуют понимания физической сущности описываемых явлений. В нашем случае, очевидно, значения всех варьируемых параметров не могут быть меньше нуля, поэтому первым элементом кортежа указан нуль. Второй элемент кортежа представляет собой список значений для каждого из варьируемых параметров.
Поскольку метод берёт на себя все расчёты, в строке 26 мы уже готовы использовать полученные значения параметров гауссианов в списке p, которые дают наиболее хорошее согласие с экспериментом. Далее осталось только построить графики и оценить погрешность аппроксимации.
Результат выполнения программы:
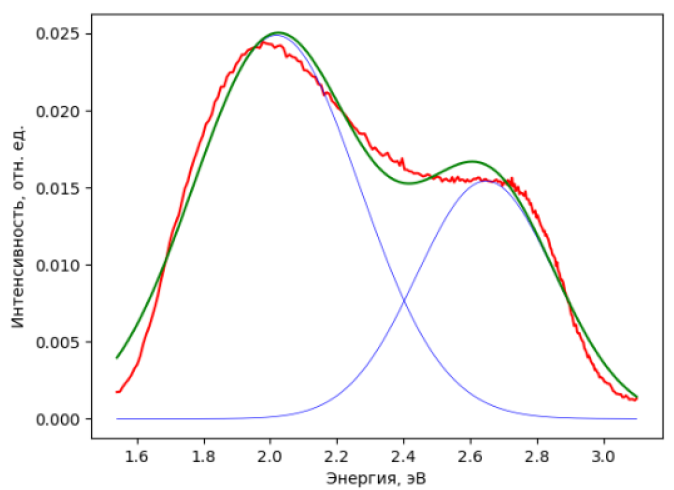
Вывод в окно терминала выглядит следующим образом:
['Лист1', 'Лист2']
Выбрали рабочий лист: Лист1
Параметры гауссианов: [0.02488419 2.01897886 0.35283369 0.01543551 2.64783453 0.2929665
Стандартное отклонение: 0.0010226334705150182
Квадрат коэффициента корреляции: 0.9779722449624711
Для оценки достоверности подгонки в строке 30 используется уже встречавшийся ранее метод std библиотеки numpy, но в научной литературе в подобных случаях обычно приводят коэффициент корреляции R, для вычисления которого можно использовать метод linregress из библиотеки scipy (строка 31, переменная r_value). Особенность linregress в том, что этот метод также считает другие статистические характеристики, и в том числе среднюю квадратичную ошибку (переменная std_err в строке 31). Таким образом, мы определяем вероятность соответствия значений YY, вычисленным с помощью функции DoubleGauss, значениям Y (эксперимент).
Несмотря на достаточно хорошую корреляцию модели с экспериментальными данными, даже визуально можно заметить систематические отклонения формы исходного спектра от полученной расчётной зависимости. Попробуем увеличить количество гауссовых пиков. Теоретически каждый новый пик с тремя новыми варьируемыми параметрами будет уменьшать погрешность модели, но в нашем случае будет физически обоснованно остановиться на сумме трёх гауссианов. Однако предполагая, что для какого-либо иного спектра может потребоваться разбиение на более чем три гауссовых пика, следующую программу напишем для аппроксимирующей функции, представляющей собой сумму любого количества гауссианов. Для этого изменим вид функции Gauss и введём новую универсальную функцию nGauss, которая сформирует сумму стольких гауссианов, на сколько хватит количества входных параметров (по три на каждый гауссиан). Функция plotAllGauss будет выводить на график каждую из гауссовых функций.
Введённые изменения никак не отразились на строках 29-38, для изменения числа гауссианов достаточно поменять число значений для списков в строках 24 и 27. Вывод графика отличается от предыдущего случая строкой 51 (показываем значение рассчитанного квадрата коэффициента корреляции) и строкой 54 (сохранение графика в png-файл).
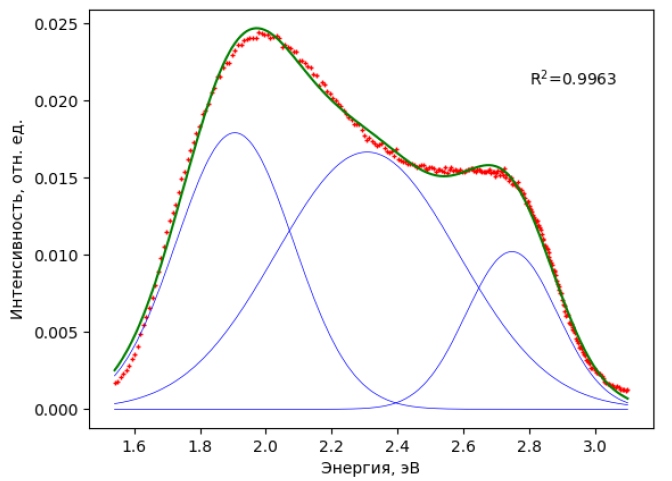
Вывод в консоль Python выглядит следующим образом:
Как можно убедиться, параметры всех трёх пиков с физической точки зрения вполне реалистичны, корреляция модели лучше, а стандартная ошибка меньше, чем в первом случае.