Глава 1. Введение в программирование Python
Numpy и Matplotlib. Оценка погрешностей измерений
Оценка погрешностей измерений, безусловно, является важной составляющей экспериментальных исследований. Рассмотрим на следующем примере, как библиотеки numpy и matplotlib справляются с такими рутинными вычислительными задачами.
Изобразим график усреднённых значений некого набора данных с указанием ошибки измерений в каждой точке:
В данном примере мы эмулируем экспериментальные данные, вычисляя sin(x) с добавлением случайной погрешности (строка 9). Количество вычисляемых точек – 20, число повторений вычислений для каждой точки – 10. В результате у нас получается numpy-матрица результатов, для которой мы можем применять необходимые статистические функции:
Для расчёта среднеарифметического значения \(\bar{Y_i}=\sum_{k=1}^N Y_k(X_i)\) для N измерений в каждой i точке используем метод mean (строка 10).
Для расчёта стандартного отклонения в каждой точке \( s_i=\sqrt{\frac{1}{N-1} \sum_{k=1}^N(Y_k(X_i)-\bar{Y_i})^2} \) возьмём метод std(строка 11).
Параметр axis=1 в нашем случае указывает, что среднее берётся по строкам. Параметр ddof определяет статистическую схему расчёта, его значение 1 соответствует несмещённой оценке дисперсии (т.е. в знаменателе стоит значение N – 1, а не N).
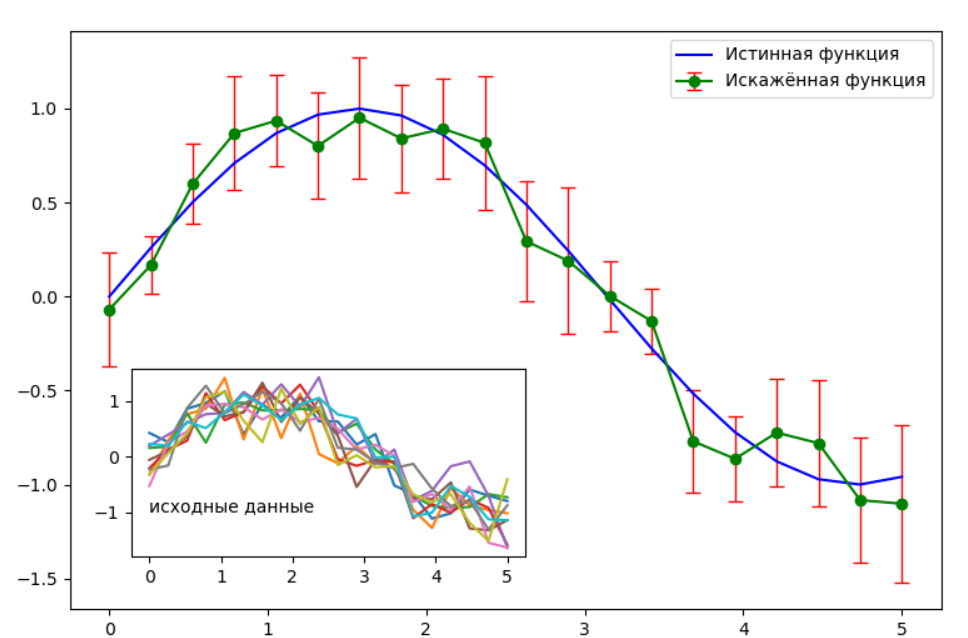
Таким образом, Y_mean и Y_std – это одномерные массивы, которые будут содержать средние значения и ошибки для всех точек. Осталось отобразить эти результаты на графике, что с успехом делает метод errorbar (строка 13), который выводит график средних значений (зелёная кривая) вместе с интервалами ошибок (красные линии) для каждой точки. Помимо параметра yerr можно использовать и xerr для отрисовки интервала ошибок по шкале абсцисс, но для нашей задачи это не требуется.
Для отображения графика исходной функции (синяя кривая) используем обычный метод plot (строка 14). Для того, чтобы показать исходный набор значений массива Y, на основном графике мы использовали врезку, которая была реализована с помощью метода axes (строка 16). Параметрами метода выступает список из четырёх значений: левый нижний угол врезки по осям X и Y, и размеры врезки dX, dY в условных единицах от 0 до 1 (единица – максимальная условная длина поля графика). Установив новые координаты, с помощью метода plot выводим всю матрицу Y на поле врезанного графика (строка 17).
Метод text выводит надпись, позицию левого нижнего угла которой следует задать в списке аргументов метода в текущей системе координат. Для того, чтобы столь сложный составной график не проиграл в разрешении, до начала всех отрисовок задаём необходимый размер поля вывода (строка 12).
При статистическом анализе результатов реальных экспериментов более корректным является расчёт стандартной ошибки среднего (средней квадратичной погрешности): \( s_i=\sqrt{\frac{1}{N-1} \sum_{k=1}^N(Y_k(X_i)-\bar{Y_i})^2} \). В этом случае достаточно умножить результат в строке 11 на \( \frac 1{\sqrt N} \), либо написать собственную функцию, вычисляющую \( s_i \) и оценку математического ожидания по заданному набору значений, как, например, это сделано в следующей программе: